Paso a paso sobre adición de fracciones homogéneas y heterogéneas
Las operaciones con fracciones es uno de los temas básicos para fortalecer el sentido numérico y el pensamiento algebraico. Aunque las fracciones hacen parte de la vida diaria de todo individuo desde los primeros años de infancia, es en la escuela donde se fortalece la resolución de problemas fraccionarios. El primer paso para lograrlo es entender su concepto y practicar operaciones básicas como la adición de fracciones.
A lo largo de este clase de matemáticas definiremos las características principales de las fracciones y los procesos primordiales para facilitar la suma o adición de fracciones homogéneas y heterogéneas.
Expresiones matemáticas: ¿Qué es una fracción?
En matemáticas, las fracciones son números que representan una porción de un todo. Esto quiere decir que son la manera en la que se expresa una unidad dividida en partes iguales. Las fracciones se conforman por un numerados y un denominador.
El numerador es aquel número que representa la cantidad de partes tomadas de la unidad dividida. En cambio, el denominador indica la cantidad de partes en las que se divide la unidad.
Ahora bien, el denominador es aquel que determinará el tipo de relación existente entre dos o más fracciones. Por ejemplo, en el caso de la adición de fracciones se deberá tener en cuenta si las fracciones tienen el mismo denominador (homogéneas) o diferente (heterogéneas)
A continuación, te explicaremos los procedimientos para hacer la adición en base a estos dos tipos de fracciones.
Así se resuelve una adición de fracciones
Adición de fracciones homogéneas
La adición de fracciones con el mismo numerador es uno de los procesos más simples y sencillos. En este proceso se deberá sumar solo los numeradores. El denominador queda igual.
Ejemplos de adición de fracciones de este estilo es:
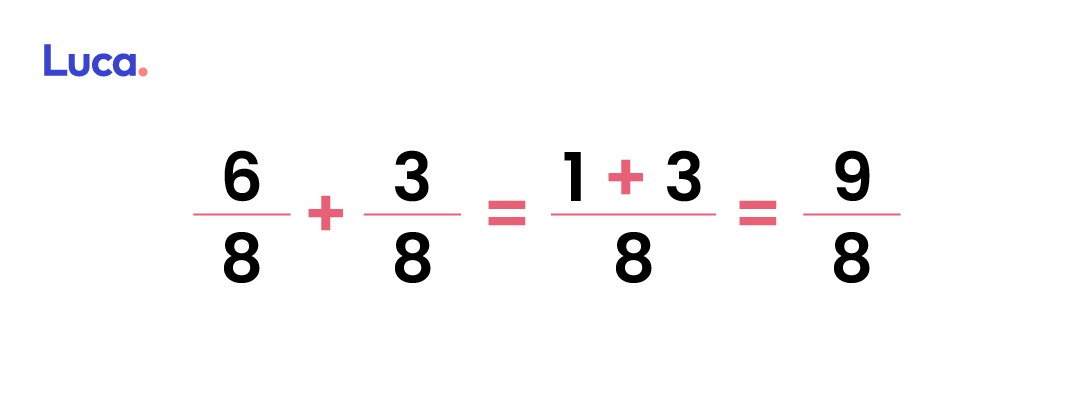
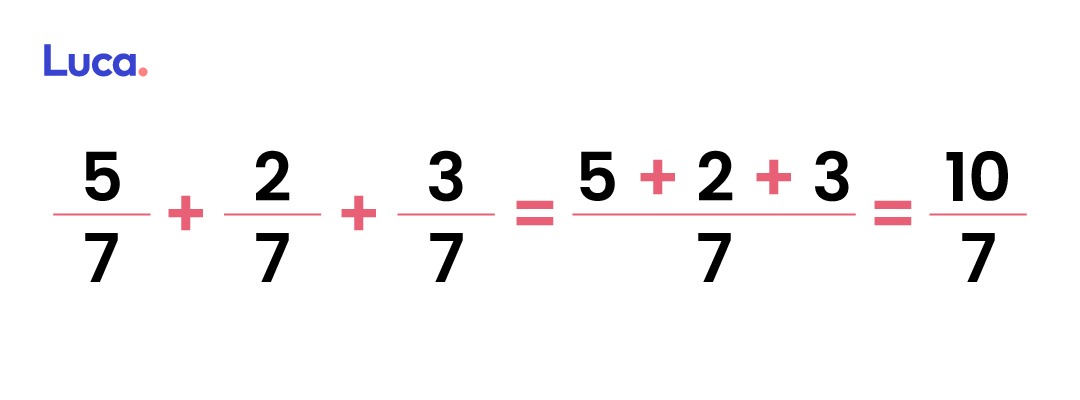
Para seguir practicando y entender a cabalidad qué es adición de fracciones homogéneas resuelve los siguientes ejercicios:
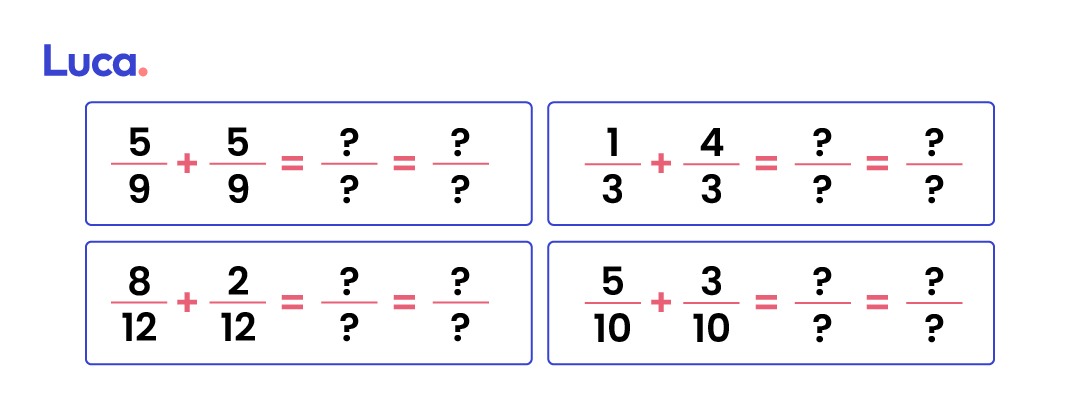
Adición de fracciones heterogéneas
En lo que concierne a la adición de fracciones heterogéneas o la adición de fracciones con distinto denominador se consideran dos métodos. El primero de ellos es encontrar el mínimo común múltiplo entre los denominadores y el segundo es el método de la multiplicación en cruz.
Adición de fracciones heterogéneas encontrando el mínimo común múltiplo
Para sumar las fracciones heterogéneas se deberá seguir los siguientes pasos:
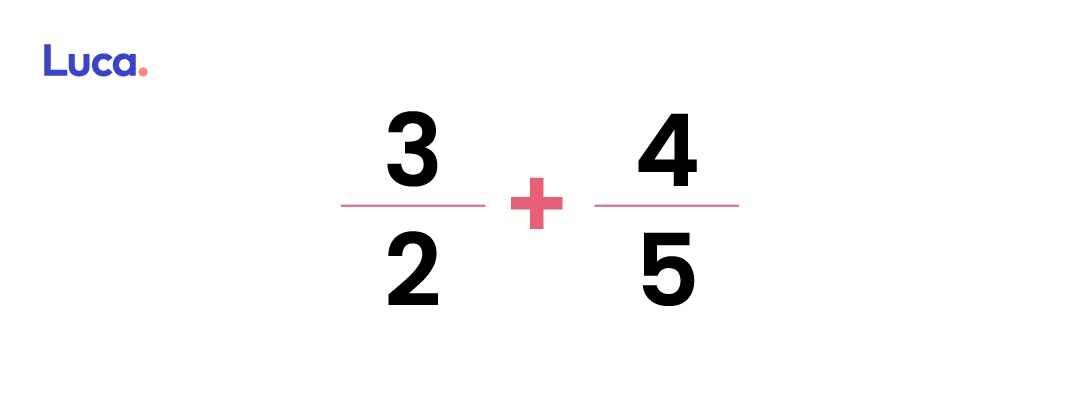
Calcular el mínimo común múltiplo de los denominadores. Para ello se deben dividir entre sus factores primos.
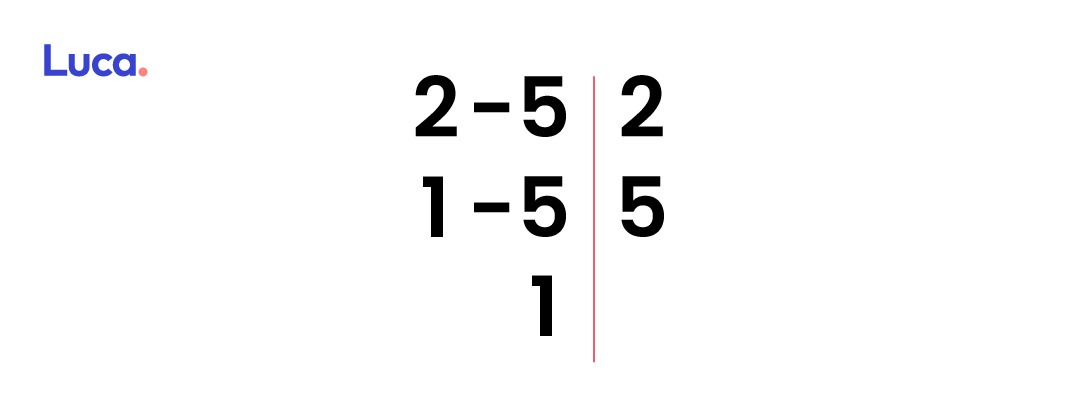
La factorización es así: la mitad de 2 es 1; 5 no tiene mitad por lo que se baja igual. Luego, al 5 se puede sacar quinta; la quinta de 5 es 1. El mínimo común múltiplo se obtiene de multiplicar los factores anteriores (2×5). El resultado es 10.
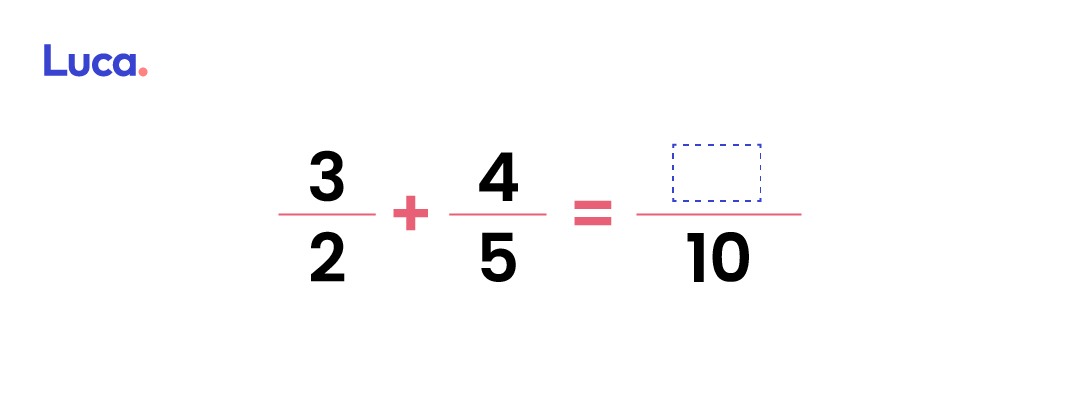
Como siguiente paso se debe dividir el mínimo común múltiplo (10) por el denominador inicial y multiplicar dicho resultado por el numerador de esa fracción:
10 ÷ 2 = 5 x 3 = 15
10 ÷ 5 = 2 x 4 = 8
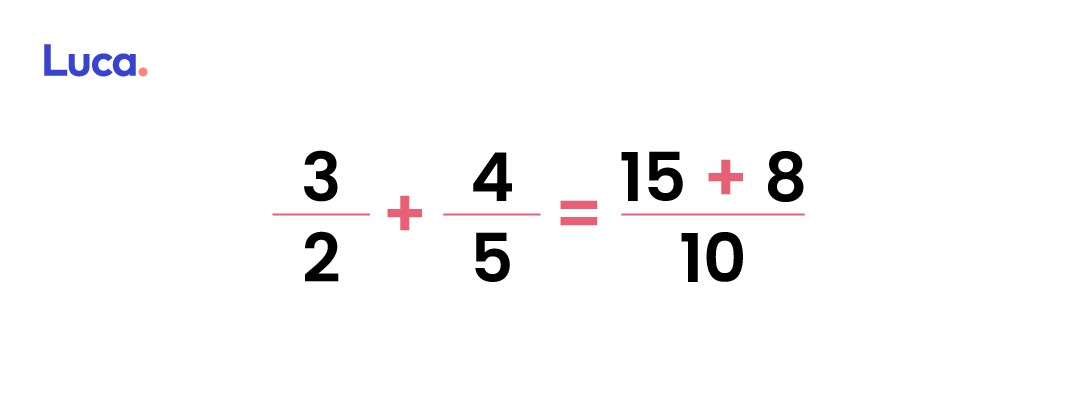
El último paso es sumar los numeradores, tal y como se haría en una fracción homogénea.
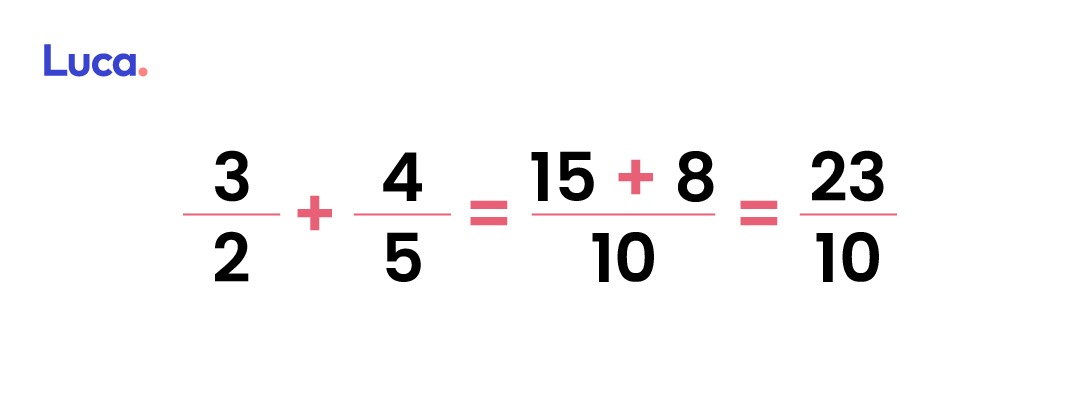
Este método funciona con la adición de tres o más fracciones.
Adición de fracciones heterogéneas por multiplicación en cruz
La operación es la siguiente:
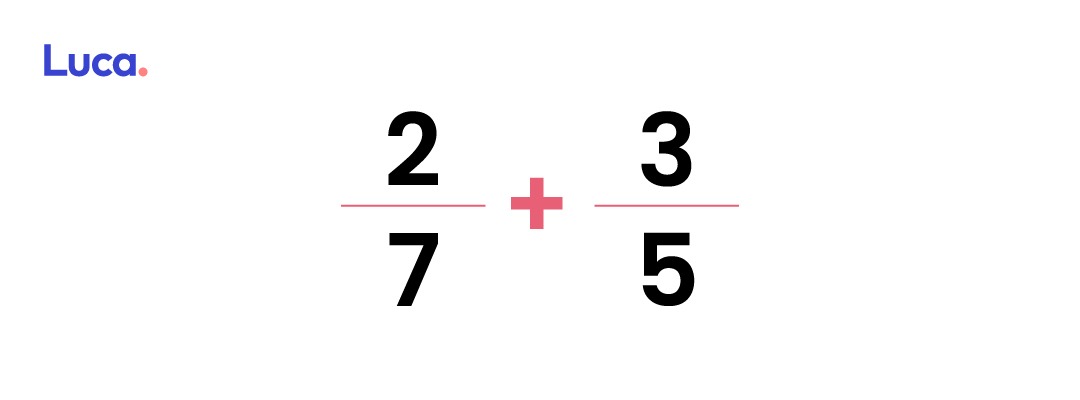
Lo primero es calcular el numerador de la fracción resultado. Para ello se deberán multiplicar las fracciones en cruz. Esto significa: el numerador de la primera (2) por el denominador de la segunda (5); luego se multiplica el numerador de la segunda (3) por el denominador de la primera (7)
El denominador de la fracción resultado se obtiene multiplicando los dos denominadores iniciales (7×5)
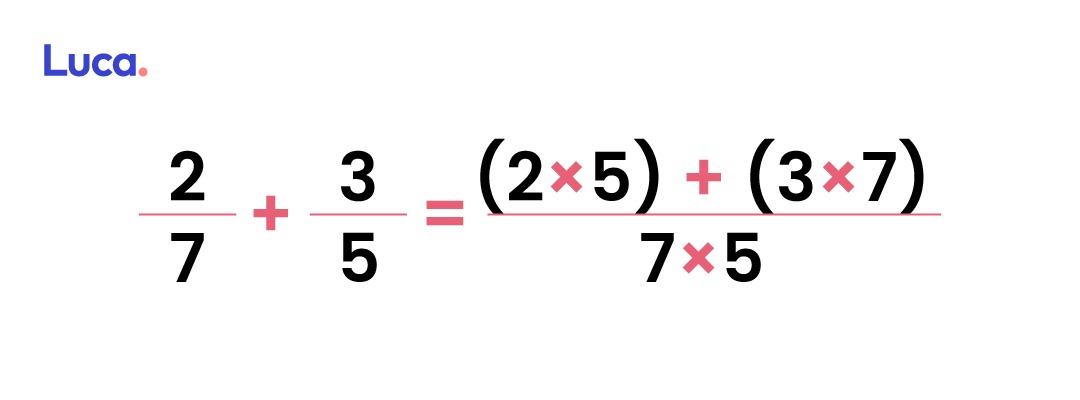
Ahora se deben resolver las multiplicaciones.
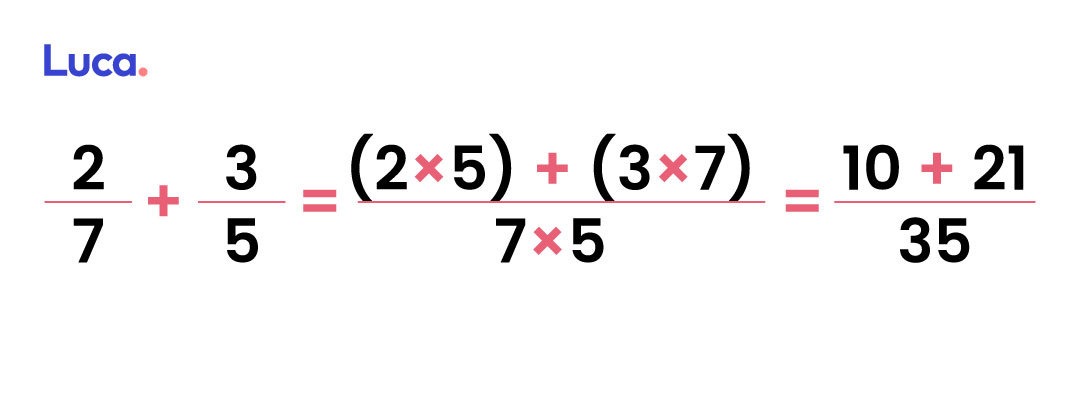
Finalmente se completa la suma de los numeradores para obtener la fracción resultado.
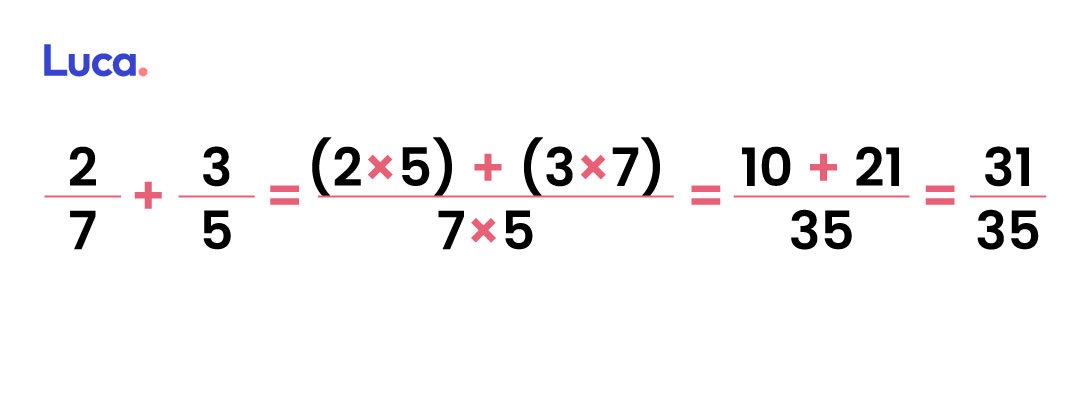
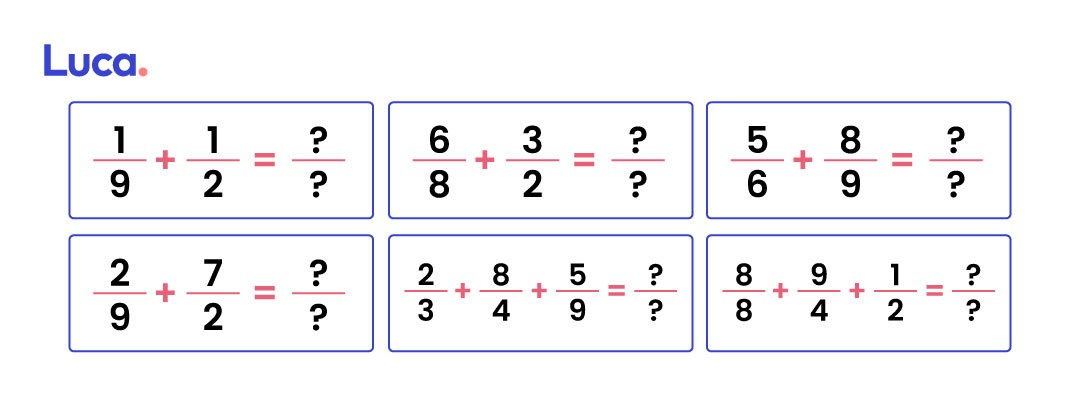
Ahora ha llegado el momento de la práctica con estos ejercicios de adición de fracciones heterogéneas:
Lo que debes tener en cuenta sobre las fracciones
- Si el numerador es un número más pequeño que el denominador, es la fracción menor a 1.
- Al ser iguales el numerador y el denominador, la fracción es igual a 1.
- En el caso de que el numerador sea más grande que el denominador, la fracción será mayor que uno.
- Si el numerador es 0, la fracción vale 0. Esto porque al dividir 0 con otro número, siempre resultará 0.
- Por el contrario, el denominador no puede ser 0. Lo anterior debido a que no es posible una división en 0.
El aprendizaje sobre adición de fracciones es clave dentro del proceso educativo. Es por eso que nuestra plataforma de aprendizaje Luca se ha convertido en la grande aliada de las escuelas para apoyar tanto a maestros como a estudiantes en áreas de matemáticas, ciencias y español y democratizar, así, la educación. ¡Conócenos aquí!




0 comentarios