Clasificación de los números: reales conceptos y ejemplos
El conjunto de los números reales es uno de los más utilizados en el ámbito de las Matemáticas y está comprendido por los números racionales e irracionales.

En esta lección de Matemáticas se explicará qué son y cómo se clasifican los números reales, así como para qué sirven.
¿Qué son los números reales y ejemplos?
En cuanto a qué son los números reales, estos consisten en cualquiera de los números que corresponda a un punto en la recta real.
Así pues, cualquier número real se encuentra comprendido entre menos infinito y más infinito, pudiendo representarse en la recta real. Se clasifican en números enteros, naturales, racionales e irracionales.
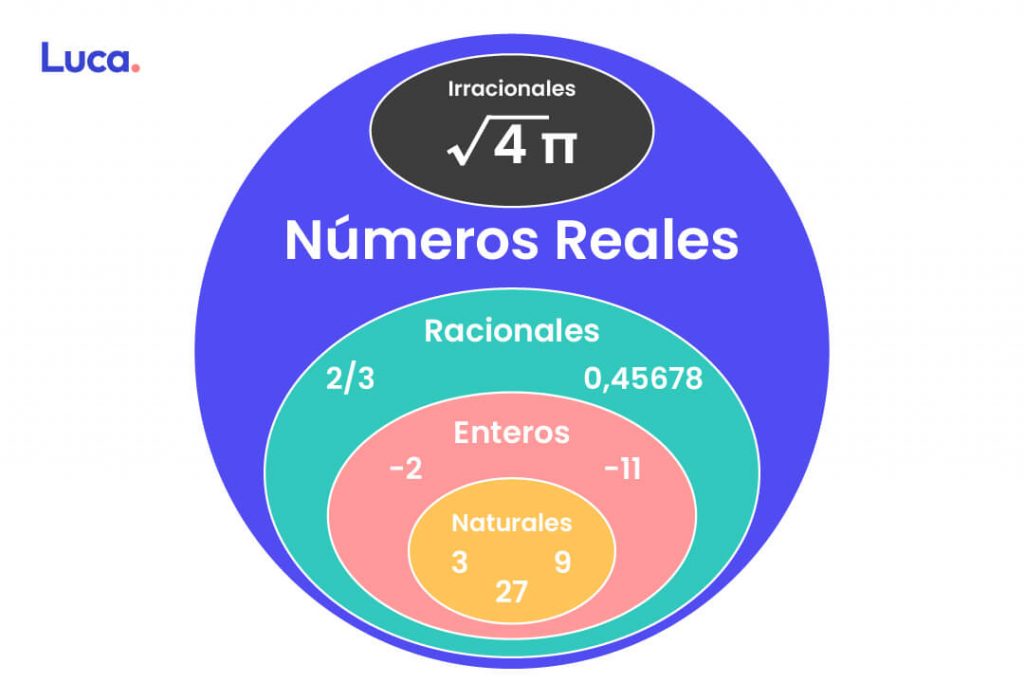
Por lo tanto, se consideran números reales a los que se encuentran comprendidos entre los extremos infinitos, de manera que, en el conjunto, no se van a agregar a los números infinitos.
Asimismo, en lo que se refiere a con qué letra se números realeslos números reales, esto es, mediante el uso de la R.
Clasificación de los números reales
En lo que concierne a la clasificación de los números reales, comprende los siguientes tipos:
Números naturales
Los números naturales se denotan con la letra N mayúscula y constituyen el conjunto de números que sirven para contar, pudiendo observarse que se encuentran compuestos por infinitos elementos.
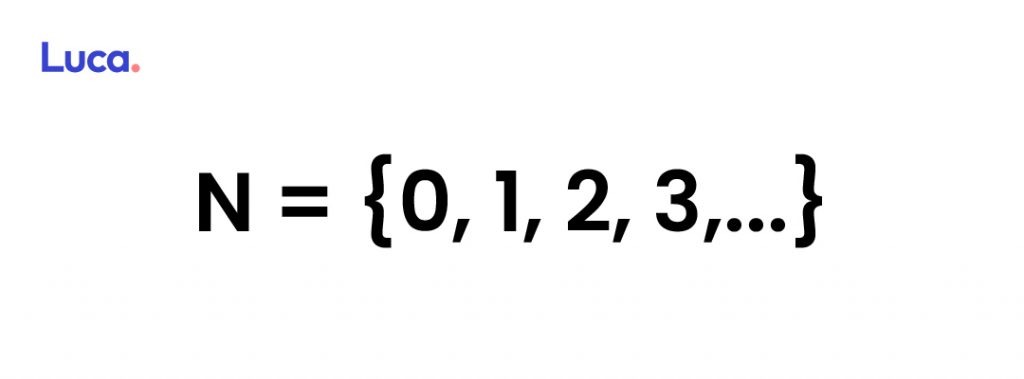
Asimismo, no hay un número natural que sea mayor que los demás.
En este sentido, para cada número natural N, existe su siguiente que se representa por N+1.
Un ejemplo de número natural es 1500, al que le sigue 1501 y después 1502 y así sucesivamente.
Números enteros
El conjunto de los números enteros se representa con una Z y se halla conformado por los naturales, así como sus opuestos, es decir, los negativos.
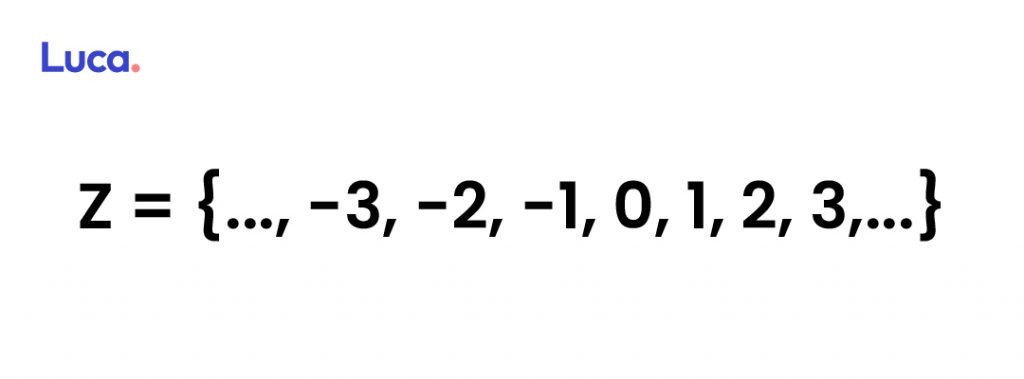
De igual modo, los números enteros comprenden el cero.
Números racionales.
Los números racionales se denotan con la letra Q mayúscula, constituyendo aquellos que están representados por el cociente de dos números enteros.

En aquellos casos en los que es necesario representar cocientes inexactos o que posean una cantidad de decimales cíclica o finita, los números racionales deben escribirse como fracciones.
Por otra parte, una fracción o número racional se encuentra conformado por tres elementos: un numerador, un denominador y un operador de cociente (/, : o ÷).
Números irracionales
Los números irracionales se representan con el símbolo I. Estos se encuentran compuestos por todos los números decimales infinitos no periódicos o dicho de otra forma, aquellas cifras cuyos decimales son infinitos y no provienen de una fracción.
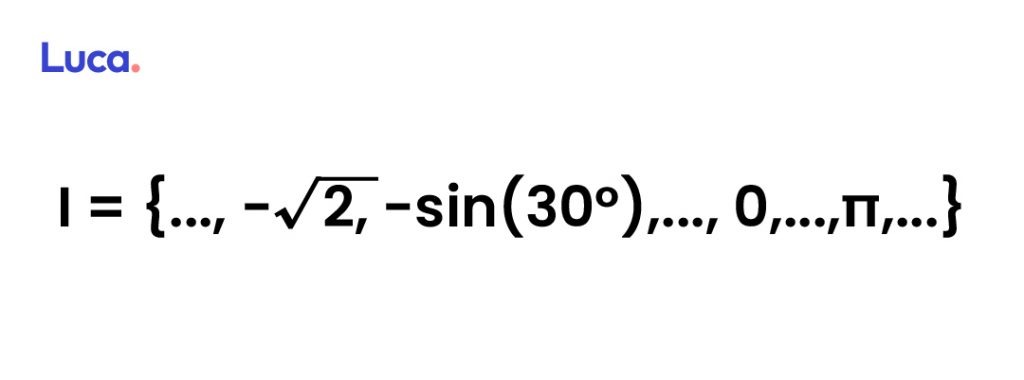
En el conjunto de los números irracionales, hay números como π y e, los cuales son constantes universales, que, no solo tienen esta forma, sino que además poseen su representación como números decimales infinitos no periódicos.
También son irracionales las magnitudes que no tienen la posibilidad de expresarse en forma entera o como fracción.
Un ejemplo de ello puede observarse en la relación de la circunferencia al diámetro de una circunferencia, que constituye el número π=3,141592…
Propiedades de los números reales
En cuanto a las propiedades de los números reales, estos se pueden emplear para realizar operaciones de suma y multiplicación.
De este modo, las propiedades de estos números son las siguientes:
Cerradura
El resultado de sumar o multiplicar dos números reales, también constituye un número real.
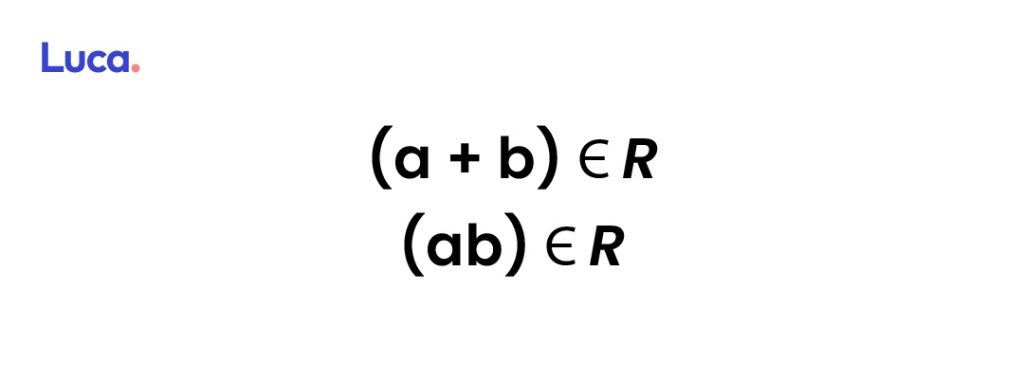
Propiedad Conmutativa
El resultado no se ve afectado por el orden al sumar o multiplicar los números reales.
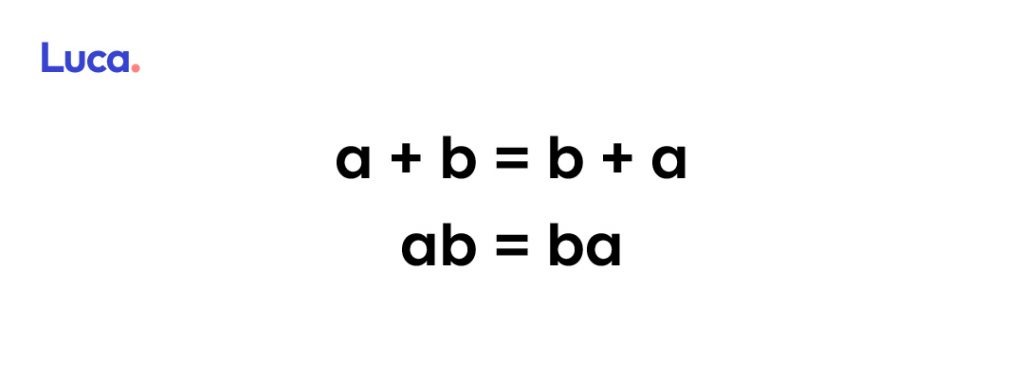
Propiedad Asociativa
Cuando se asocia la suma o multiplicación de tres o más número reales, no importa el orden, debido a que, el resultado siempre será el mismo.
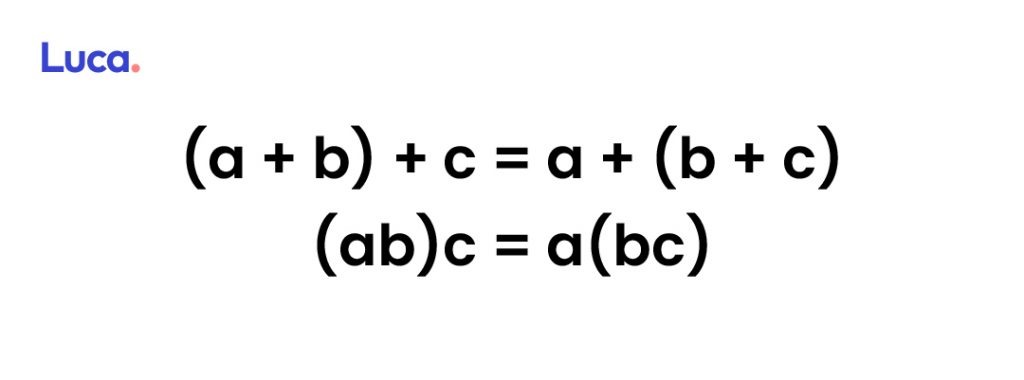
Elemento Neutro
En el caso de la adición, cuando a un número real se le suma el cero (neutro aditivo), ese se queda igual.
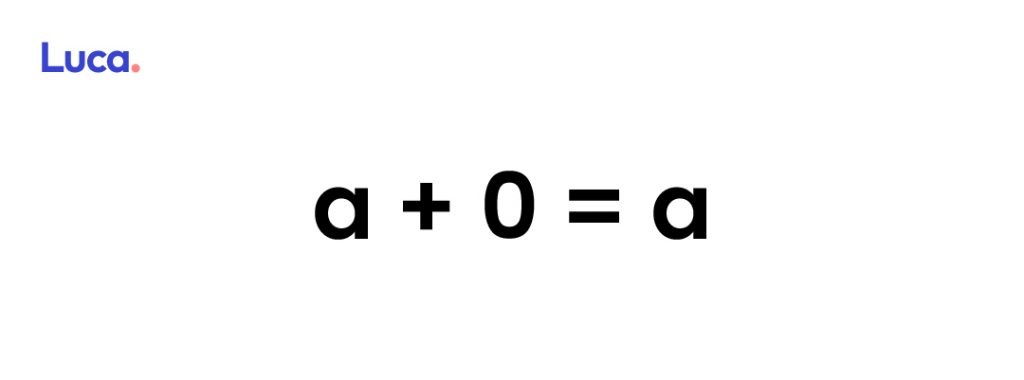
Al tratarse de la multiplicación, si un número real se multiplica por 1, este permanece igual.
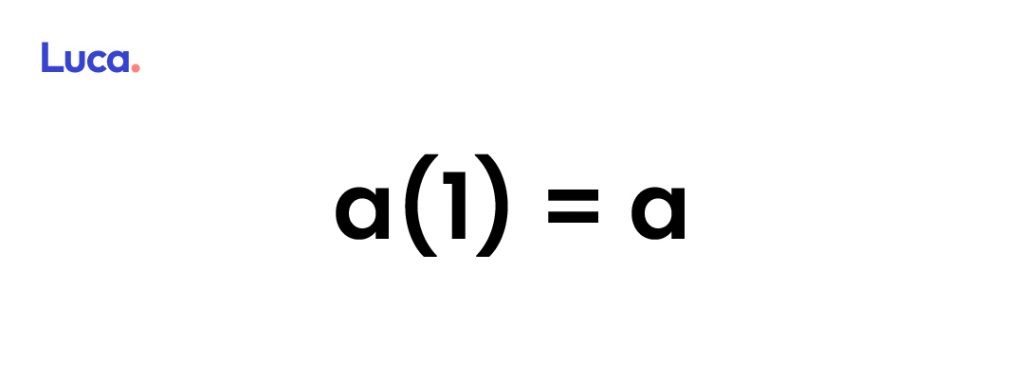
Inverso
Con relación a la adición, cuando se le suma su inverso a un número, se obtiene como resultado el 0 (neutro aditivo).
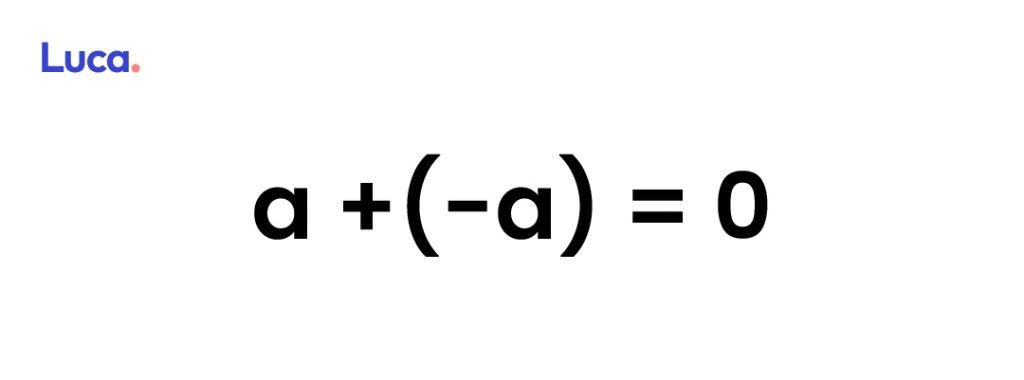
En lo que se refiere a la multiplicación, cuando se multiplica por su inverso multiplicativo un número, el resultado será 1 (neutro multiplicativo).
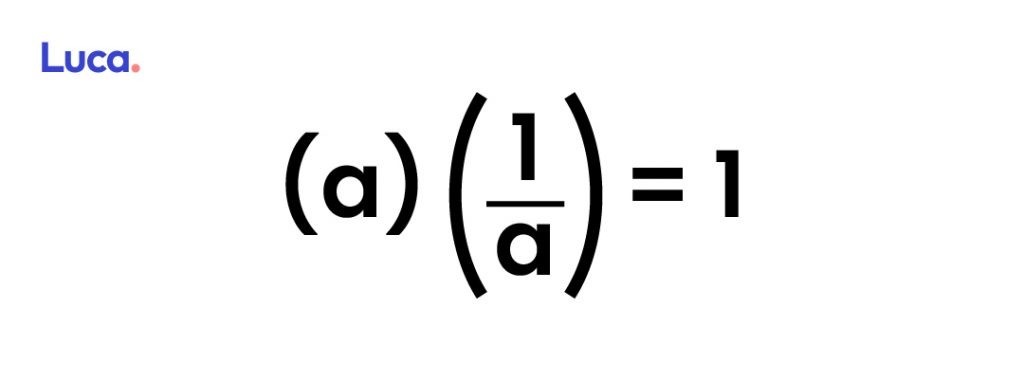
Ejercicios de números reales
Los siguientes ejercicios de números reales permitirán comprender de qué forma se pueden emplear para resolver problemas y diferentes circunstancias que puedan presentarse en la vida diaria.


¿Para qué sirven los números reales?
En cuanto a la interrogante acerca de para qué sirven los números reales, estos permiten representar números positivos y reflejar grados sobre cero, distancias a la derecha, ganancias, así como, representar números negativos y mostrar pérdidas, deudas, distancias a la izquierda y grados bajo cero, entre diversas acciones en las que es vital utilizar esta clase de números en particular.
¿Cuándo los números no son reales?
Los números que no son reales son los números imaginarios, que fueron aceptados en el ámbito de las Matemáticas aproximadamente en 1780, empleándose en la Física y la Ingeniería. Estos se basan en el número «i» , que es la raíz cuadrada de −1.
Algunos ejemplos de los números imaginarios son i,3+4i,−8i, entre otros.
Con respecto a los números reales, es importante tener en cuenta los siguientes aspectos:
- Con los números reales pueden realizarse todas las operaciones, salvo la radicación de índice par y radicando negativo, así como la división por cero.
- Todos los números reales están representados por un punto de la recta, mientras que, a todo punto de la recta, también le corresponde un número real.
- En la recta real, el orden de los números se conoce por la posición que tengan en esta, de modo que, mientras más a la derecha se encuentra un número, puede ser más grande, siendo menor en la medida que este se halle más la izquierda.
- El conjunto de los números reales posee una cantidad infinita de elementos, es decir, que estos no tienen final, bien sea que se trate del lado positivo o el negativo.
Luca facilita el aprendizaje de los números reales
La plataforma educativa Luca es un entorno virtual de aprendizaje que contribuirá a que los estudiantes puedan desarrollar habilidades para realizar ejercicios de números reales y aprender esta temática de Matemáticas de Educación Primaria de una forma más rápida y efectiva.

Si desea que los estudiantes de su institución educativa o sus hijos puedan disfrutar de las ventajas que ofrece esta herramienta digital, puede registrarse en el siguiente enlace.




0 comentarios