Cómo hacer particiones con el Diagrama de Young y el Diagrama de Ferrers

La teoría de las particiones puede emplearse en diferentes aspectos de la vida diaria, debido a que, permite determinar las diferentes maneras en las que se puede descomponer un número entero en sumandos, lo que puede ser muy útil al tener que dividir algún elemento en partes.

 

 

En esta lección de Matemáticas se expondrá qué son las particiones y cuáles son los tipos que hay.

 

 

¿Qué es una partición?

 

 

Con respecto a la interrogante de qué es una partición de un número entero positivo n, se trata de un modo en el que esta cifra puede descomponerse a través de una suma de números enteros positivos.

 

 

 

 

 

 

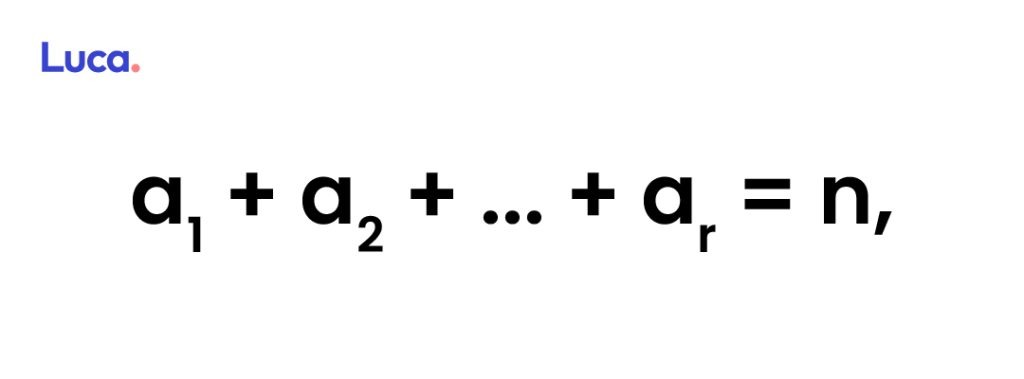
Por ejemplo, p (6) = 11 porque el número entero 6 posee las once siguientes particiones:

 

 

 

 

De este modo, el cálculo de p (n) se lleva a cabo de la siguiente manera:

 

 

 

 

 

 

Así pues, p (6) =11

 

 

¿Para qué sirven las particiones?

 

 

En lo que concierne a la interrogante acerca de para qué sirven las particiones de números, estas pueden ser empleadas en el estudio de grupos simétricos, polinomios simétricos, al igual que en teorías de representación de grupos, entre otros.

 

 

¿Cómo hacer una partición?

 

 

Existen 2 métodos a través de los que es posible representar las particiones de una manera sencilla.

 

 

Por un lado, se encuentra el diagrama de Ferrers, que fue nombrado por Norman Macleod Ferrers y el diagrama de Young, que se renombró después por el matemático británico Alfred Young.

 

 

Para esto, hay que emplear la notación inglesa con esquemas alineados en la esquina superior izquierda.

 

 

Así pues, el modo de cómo hacer una partición consiste en hacer la suma de los respectivos números, colocándolos de mayor a menor.

 

 

No obstante, no es obligatorio poner los números de esta manera al representar las particiones.

 

 

Diagrama de Young

 

 

Una manera de hacer particiones es mediante el uso del diagrama de Young, en el que se lleva a cabo un arreglo de las casillas ubicadas por filas, haciendo que cada fila tenga una cantidad que sea menor o igual que las casillas de la fila anterior.

 

 

De ese modo, es posible tener una sucesión de enteros positivos que cuente con las características de una partición.

 

 

Cada fila constituye un elemento de la partición en el diagrama, mientras que, el número completo de cuadros comprende el valor de n.

 

 

 

 

En el ejemplo que se da a continuación se puede observar la partición de p (8) = 4 + 2 + 1 + 1 según el método del Diagrama de Young

 

 

 

 

 

 

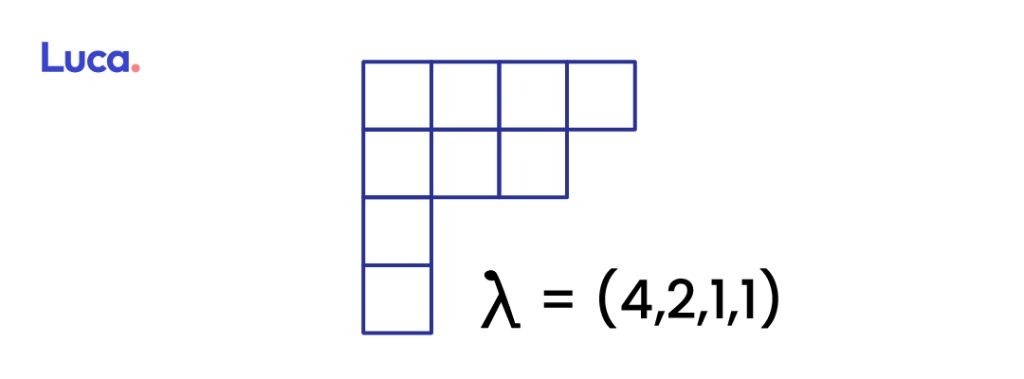
Diagrama de Ferrers

 

 

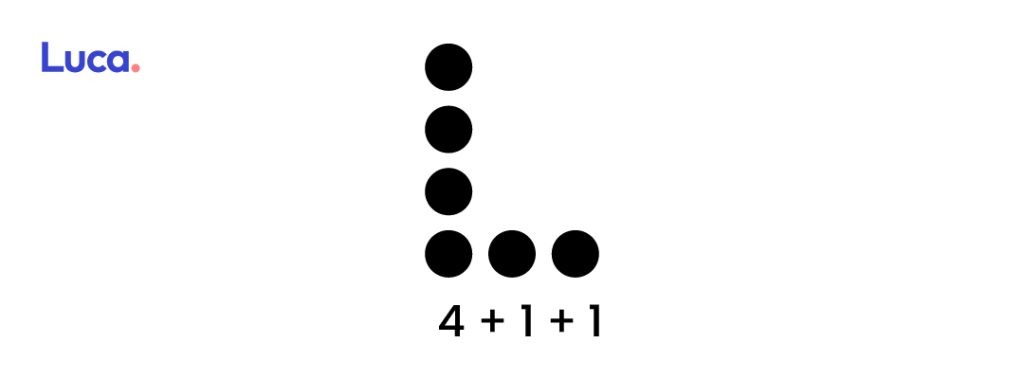
Una partición de n se puede representar mediante un diagrama de Ferrers , que consiste en una matriz de puntos, que posee tantas filas como sumandos no nulos hay en la partición, y a su vez, en cada fila pueden observarse tantos puntos como el valor que tiene el sumando.

 

 

En vista de que no cuenta el orden de los sumandos, el diagrama puede disponerse de tal forma que las filas se hallen en orden no decreciente de sus longitudes, encontrándose ubicadas de arriba hacia abajo.

 

 

En el p (6) = 11 se pueden observar las siguientes particiones según el método del Diagrama de Ferrers :

 

 

6

 

 

 

 

5+1

 

 

 

 

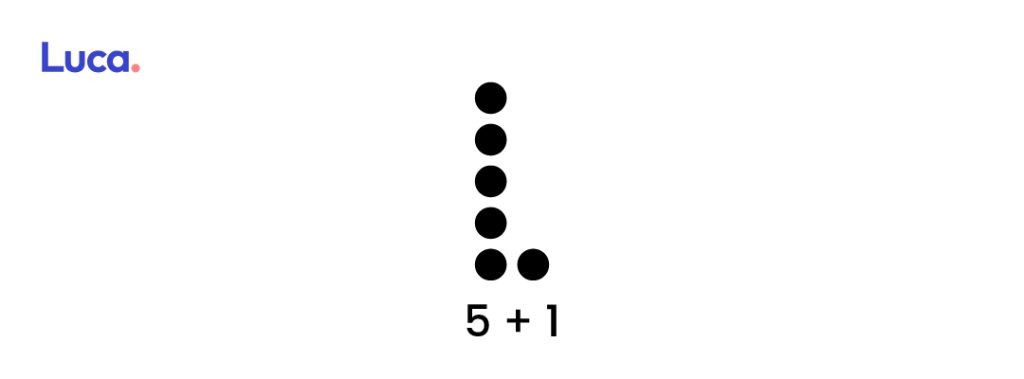
4+2

 

 

 

 

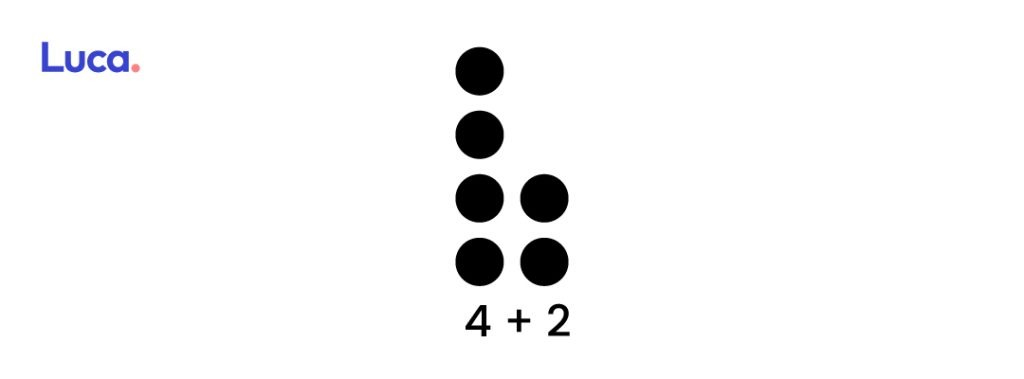
4 + 1 + 1

 

 

 

 

 

 

3+3

 

 

 

 

 

 

3+2+1

 

 

 

 

 

 

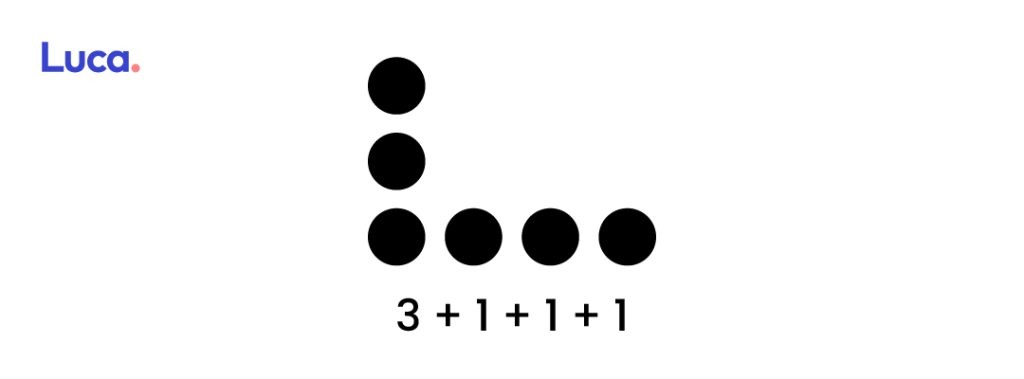
3+1+1+1

 

 

 

 

 

 

2+2+2

 

 

 

 

 

 

 

 

2+2+1+1

 

 

 

 

 

 

2+1+1+1+1

 

 

 

 

 

 

1+1+1+1+1+1

 

 

 

 

 

 

Con respecto a la teoría de particiones, es importante tener en cuenta los siguientes aspectos:

 

 

• La función de partición >p>(n) permite indicar el número de posibles particiones del entero n.
• Aunque no es relevante el orden de los sumandos en las particiones, por lo general, estas se escriben de mayor a menor.

 

 

La Plataforma Educativa Luca facilita el aprendizaje de Matemáticas

 

 

En la Plataforma Educativa Luca, los niños de Primaria pueden aprender de una forma fácil, divertida y rápida contenidos programáticos de Matemática, Español y Ciencias.
Si desea que los estudiantes de su institución o hijos puedan disfrutar de todos los beneficios de esta herramienta educativa innovadora, puede registrarse en el siguiente enlace.