Papel de las fracciones de longitudes y de superficies de figuras con ejemplos
Entre las muchas temáticas que hacen parte de las clases de matemáticas en primaria, las lecciones acerca de fracciones suponen alta importancia. Comprenderlas es fundamental para desarrollar el sentido numérico y el pensamiento algebraico. Para sacar el máximo provecho a esta temática se deberán abordar temas como la suma y resta de fracciones, las fracciones equivalentes o, el tema de la clase de matemáticas de hoy: fracciones de longitudes y de superficies de figuras.
Acompáñanos a lo largo de esta lección y conoce más sobre este tema fundamental.
Paso a paso: Fracciones de longitudes y de superficies de figuras
¿Cómo se mide la longitud en fracciones?
Para responder a esta pregunta, se debe partir de la definición de longitud. Así, la longitud es la distancia que hay entre dos puntos cualquiera. Su unidad de medida es el metro, en el sistema métrico decimal; también puede representarse en Kilómetros y centímetros.
Ahora bien, cuando necesitamos obtener una medida de longitud que es menor que 1 (unidad) se hace necesario recurrir a las fracciones. Ellas ayudarán a llegar a resultados más precisos.
Ejemplos de longitud de fracciones
Para saber medir la longitud en fracciones te puedes basar en el siguiente ejemplo, utilizando al metro.
Para comenzar, deberás saber que el metro representa la unidad. Ahora, un metro significa 100 cm (centímetros), también significa 1000 mm (milímetros) y 10 dm (decímetros). Para dividir el metro en fracciones se hace lo siguiente:
- Para dividir la unidad en dos (1/2) deberás dividir 100 cm en 2 (50). También podrás dividir los 1000 mm (500 mm). Estos resultados reflejan 1/2 de metro.
- Ahora bien, al dividir la unidad en cuatro partes iguales, deberás dividir 100 o 1000 en 4. Esto da como resultado que 1/4 de metro corresponde a 25 cm o 250 mm, respectivamente.
- Si lo que se quiere es dividir la unidad en más partes iguales, es por ejemplo en 1/10, se tendrá que dividir 100 o 1000 entre 10. Esto da como resultado 10 cm o 100 mm, respectivamente.
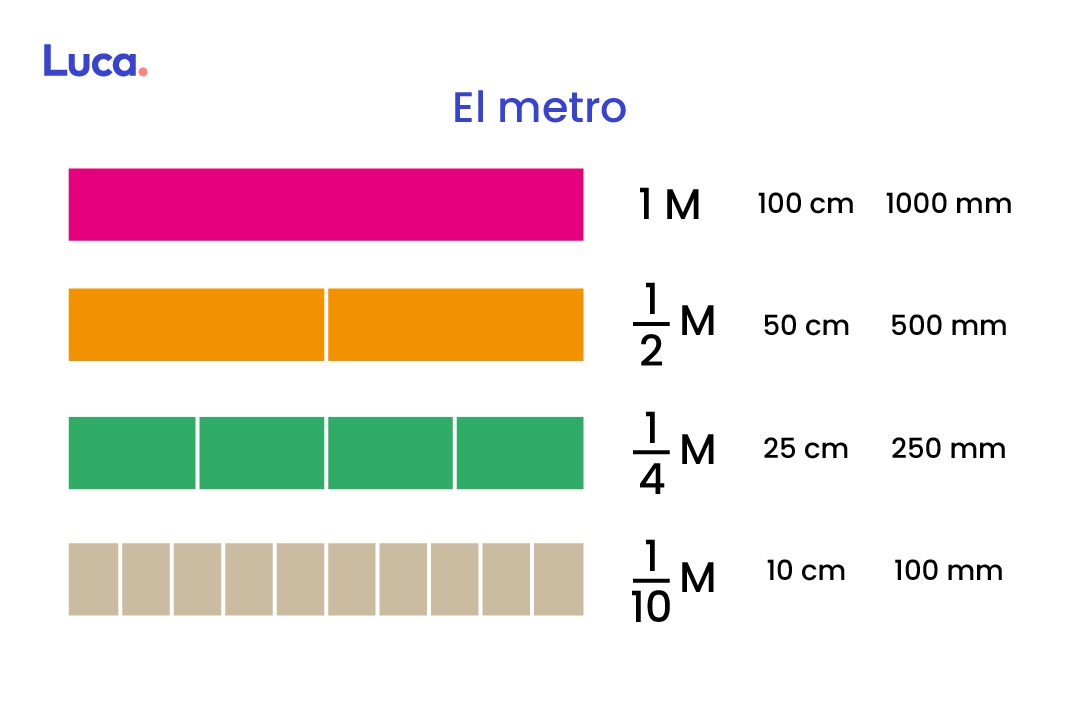
Recuerda que cuando se divide una longitud en fracciones iguales, al sumar dichas fracciones obtendrás la unidad completa.
¿Qué es la superficie de una figura para niños?
De las fracciones de longitud y de superficies de figuras ya está la primera parte clara. Solo resta entender lo relacionado con superficie, pero ¿Cuál es la superficie de una figura? Partamos por saber que la medida de la superficie es el área, es decir, la porción de plano que ocupan las figuras y esta se representa en cuadradas de longitud.
Para saber cómo se calcula la superficie de una figura se deberán tener en cuenta las siguientes fórmulas:
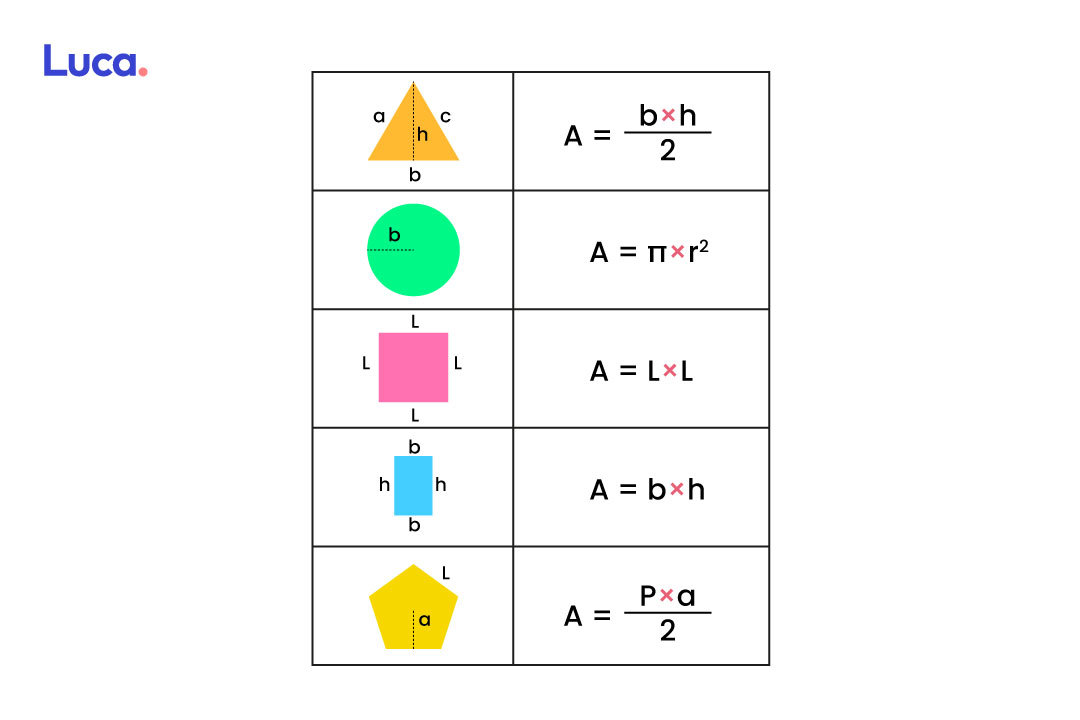
Ejemplos para calcular la superficie de figuras con fracciones
Comencemos con los cuadrados. Supongamos que uno de los lados del cuadrado mide 6/20. Como en el cuadrado todos los lados miden lo mismo, para calcular el área se deberá multiplicar lado x lado, es decir, 6/20 x 6/20, así:
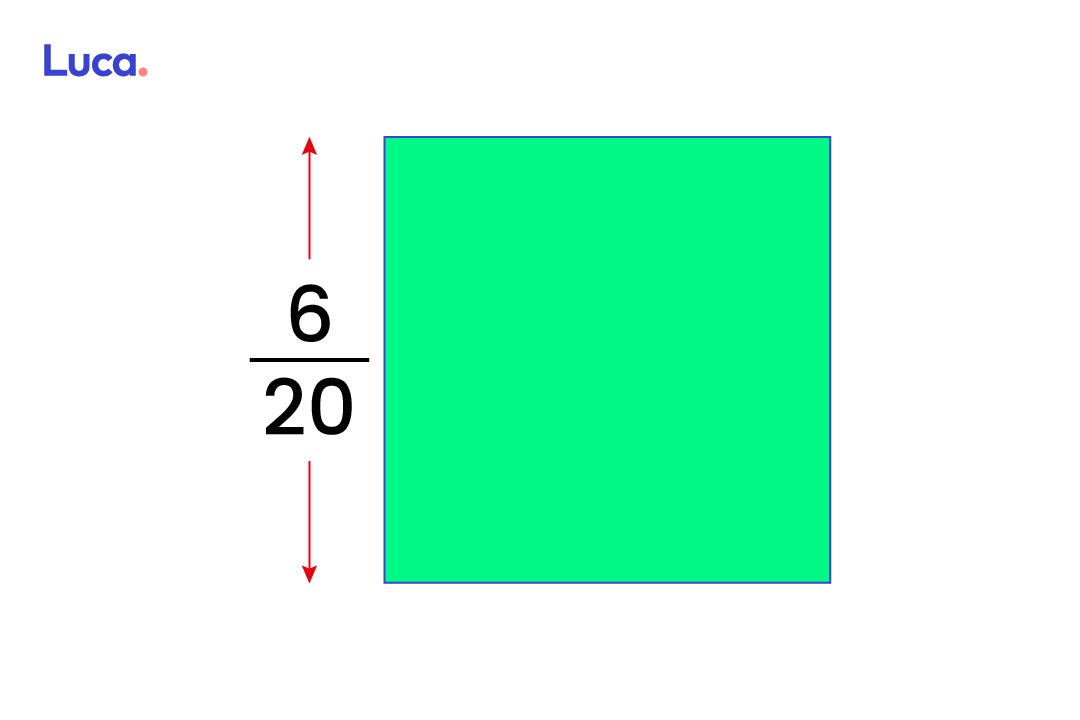
NOTA: La multiplicación de fracciones se hace de manera directa (numerador con numerador y denominador con denominador)
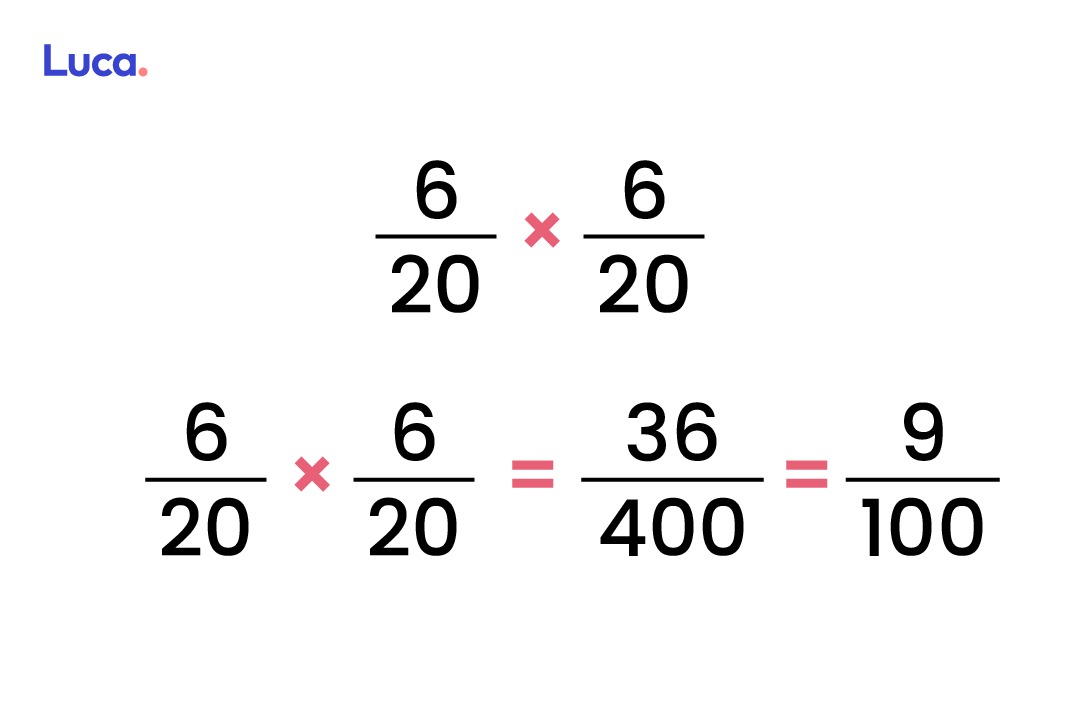
Al hacer la multiplicación se obtiene como resultado 36/400. Para lograr un mejor resultado, se procede a simplificar la fracción dividiendo numerador y denominador en 2. De esta manera, el área del cuadrado es 9/100 unidades cuadradas.
Otro gran ejemplo es encontrar el área de un triángulo. Para obtenerla se debe utilizar la fórmula: base x altura/2. En este caso, la base del triángulo será de 5/2, y la altura de 2/5.
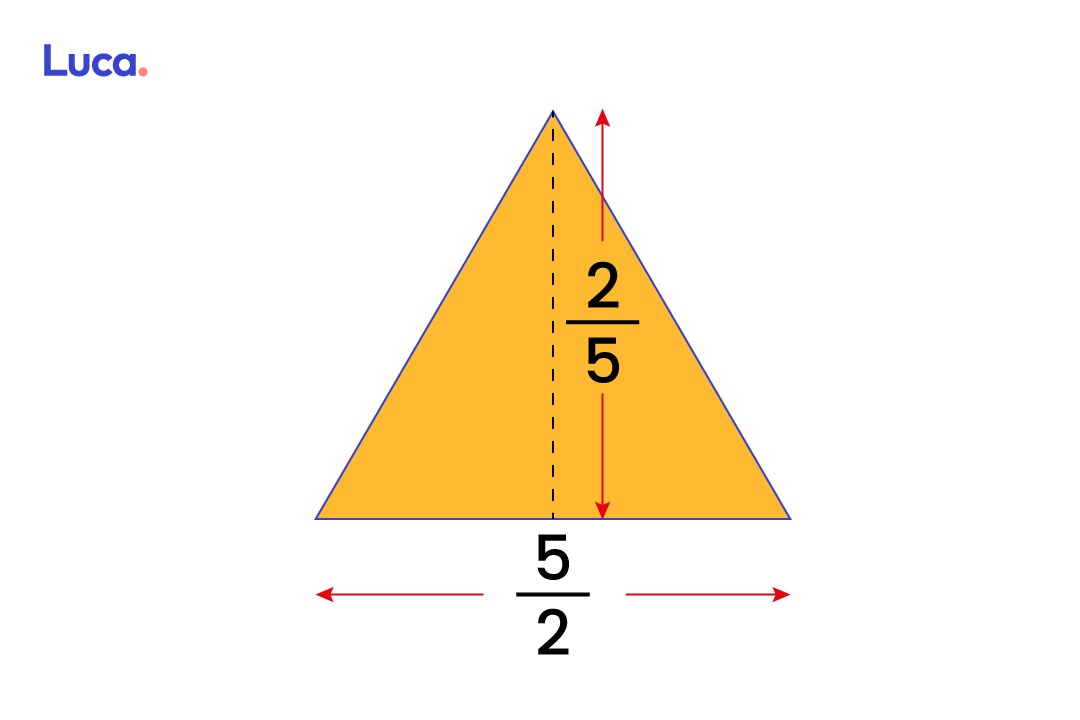
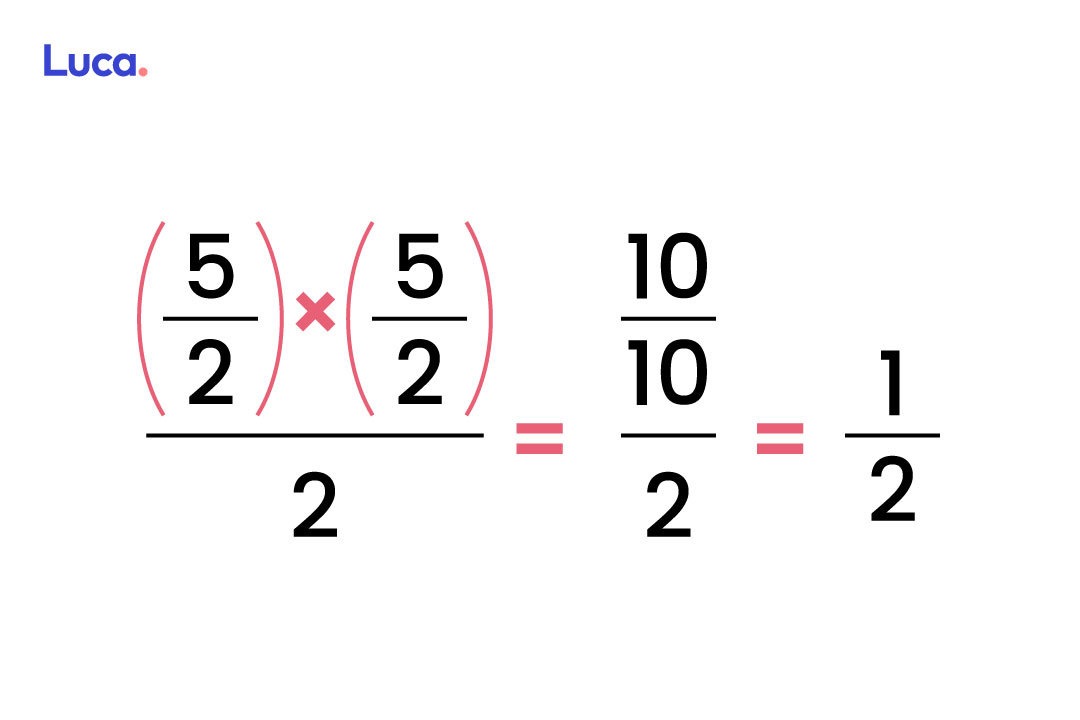
En este caso, la multiplicación resultó en 10/10, lo que implica un entero que se representa en 1 unidad. Dicha unidad se divide en dos y, al no poder simplificarse más, se llega al resultado de que el área del triangulo es de 1/2 unidades cuadradas.
Antes de culminar con las fracciones de longitudes y de superficies de figuras recuerda que es fundamental repasar todo lo relacionado con las operaciones básicas de fracciones, además de recta numérica y figuras geométricas. En Luca queremos ayudar a las escuelas y, por tanto, a sus estudiantes a reforzar estas temáticas de manera sencilla y divertida. Por eso, ofrecemos a las instituciones educativas los materiales, recursos y acompañamiento adecuado para lograrlo. ¡Conócenos aquí!




0 comentarios