Características y ejemplos de la tabla de derivadas
Dentro de los conocimientos y aprendizajes fundamentales de las lecciones de matemáticas, especialmente en lo relacionado con el análisis y representación de datos, saber qué son las derivadas cumple un papel esencial. Este concepto, además, derivará en la comprensión de otros más complejos como el cálculo diferencial, el cálculo infinitesimal, las variables independientes, entre otros. Es por ello por lo que en esta lección aprenderás todo sobre ellas, a partir de la tabla de derivadas.

Ya sabes cómo sumar, multiplicar y dividir. Ya conoces las fracciones, los decimales y los números romanos. Ahora es momento de aumentar la complejidad y disfrutar de este apasionante tema. Así que…¡Vamos por ello!
Para entender la tabla de derivadas hay que entender qué son las derivadas
El primer paso para entender qué son las tablas de derivadas o cómo usarlas, debemos partir del concepto de derivada. Las derivadas son parte clave dentro de las funciones. Estas últimas se refieren a la relación entre dos valores. Una relación dependiente: cada valor depende del otro. En razón de lo anterior, la derivada de una función matemática se refiere a la velocidad de cambio del valor de dicha función, de acuerdo con la manera en la que se modifique la variable independiente que la conforma.
De esta forma, las derivadas ─representadas en la tabla de derivadas─ sirven para estudiar las funciones. Ellas se expresan a través del signo prisma (‘). Si la función es f(x), la derivada de esta sería f‘(x). Para calcular la derivada de una función se aplican reglas de acuerdo a la función a analizar. Esto con ayuda de la tabla de derivadas, de la que hablaremos más adelante.
Tipos de derivadas según la función de la que provienen
Derivada de una constante
Esta siempre será igual a 0. El resultado es independiente del valor de la variante.
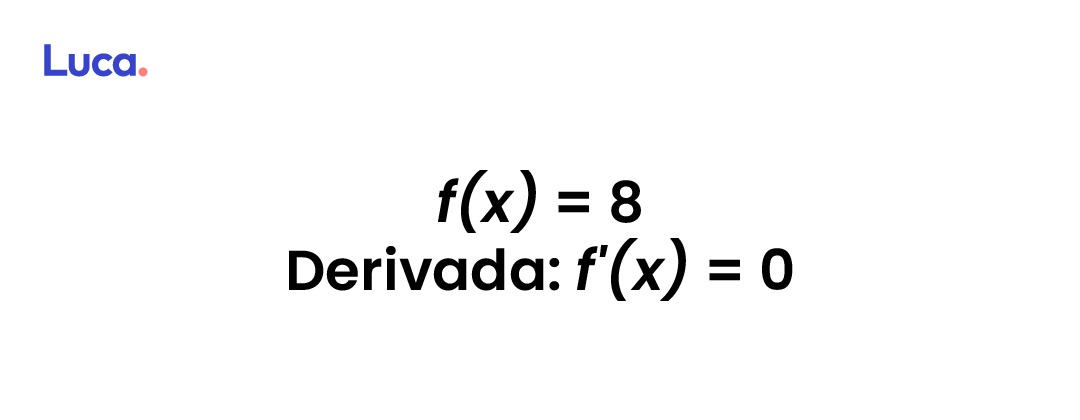
Derivada de una función lineal
El resultado de la función derivada será el coeficiente del término de primer grado. Así:
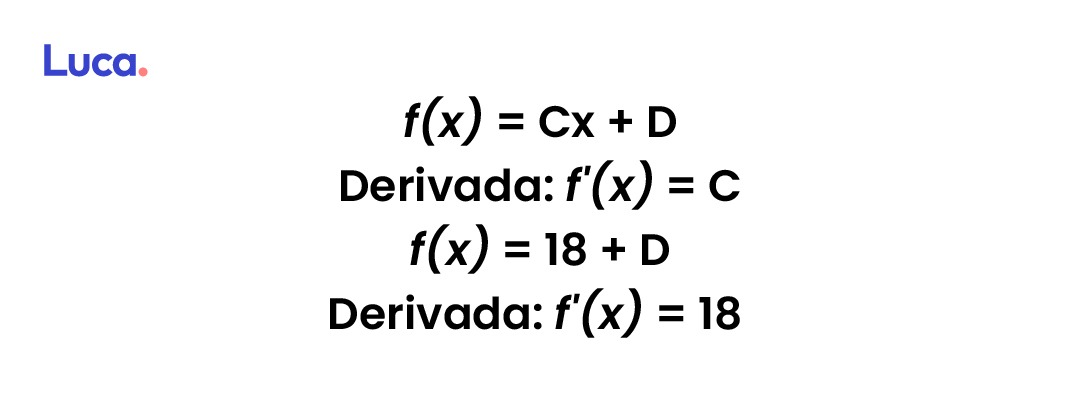
Derivado de una potencia
Para encontrar esta derivada se deberá realizar la multiplicación de la función por el exponente y restarle a este una unidad. De la siguiente forma:
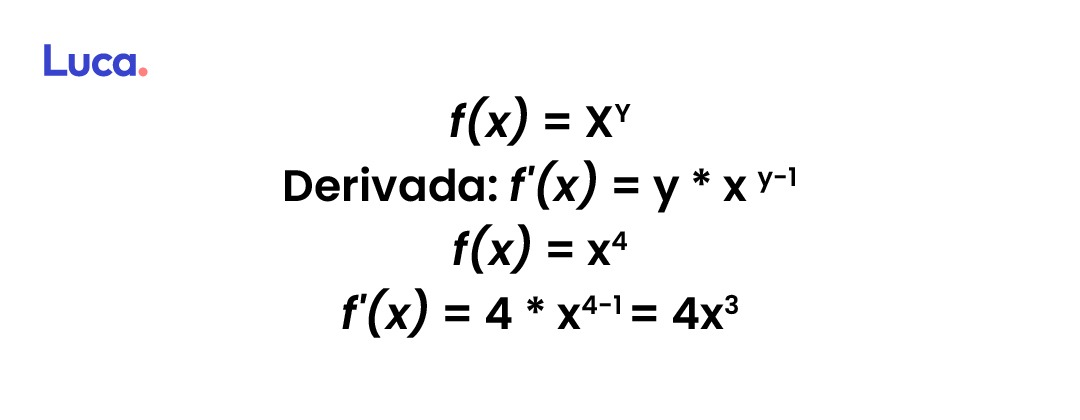
Derivada de una raiz
Considerada como una función irracional, el producto de esta derivada es igual a uno. Este se parte por el producto del índice de la raíz, multiplicándolo por la misma raíz y restándole uno al exponente del radicando.
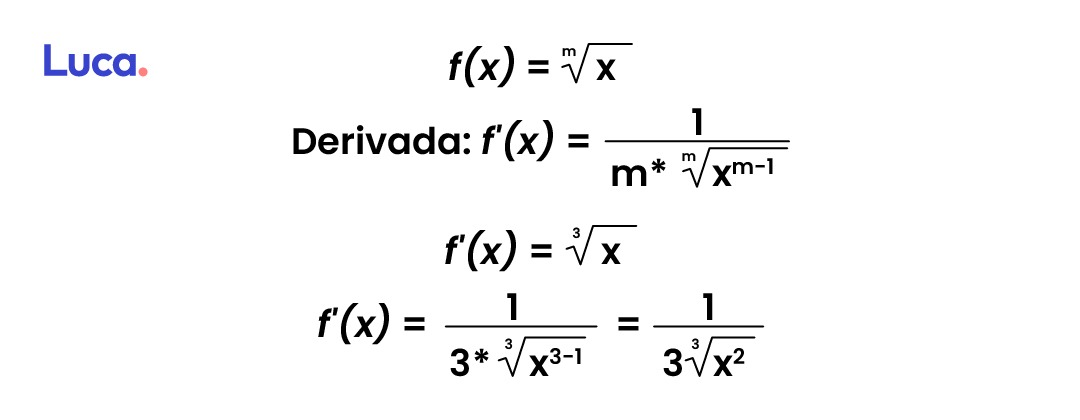
Derivada de una función exponencial
La solución de esta derivada dependerá de si su base es el número e o si es otro número. Partiendo de esto, hay dos formas de resolver estas funciones:
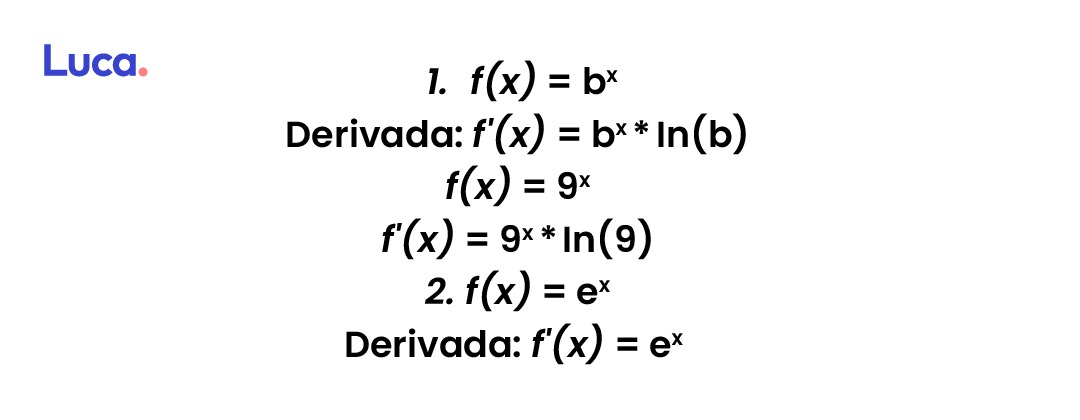
Derivada de una función logarítmica
En este caso, al igual que el anterior, la derivada dependerá de la base del algoritmo; si este es natural o la base es otro número la regla cambia.
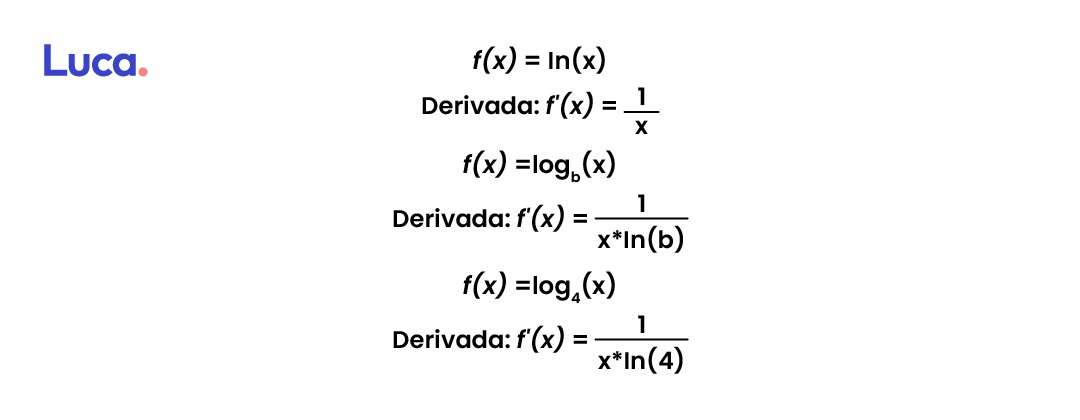
Derivadas trigonométricas
Estas son función seno, función coseno y función tangente.

¿Qué son las tablas de derivadas y quién las creo?
Las tabla de derivadas fue creada por Charles Goodheart e introducida en la London School of Economics en 1947. Esta ayudará a determinar el valor de una derivada y predecir así el comportamiento de una determinada ecuación. Generalmente la tabla de derivadas presenta las funciones más usadas y sus derivadas.
A continuación, te dejamos un ejemplo de ellas, con las funciones mencionadas anteriormente:
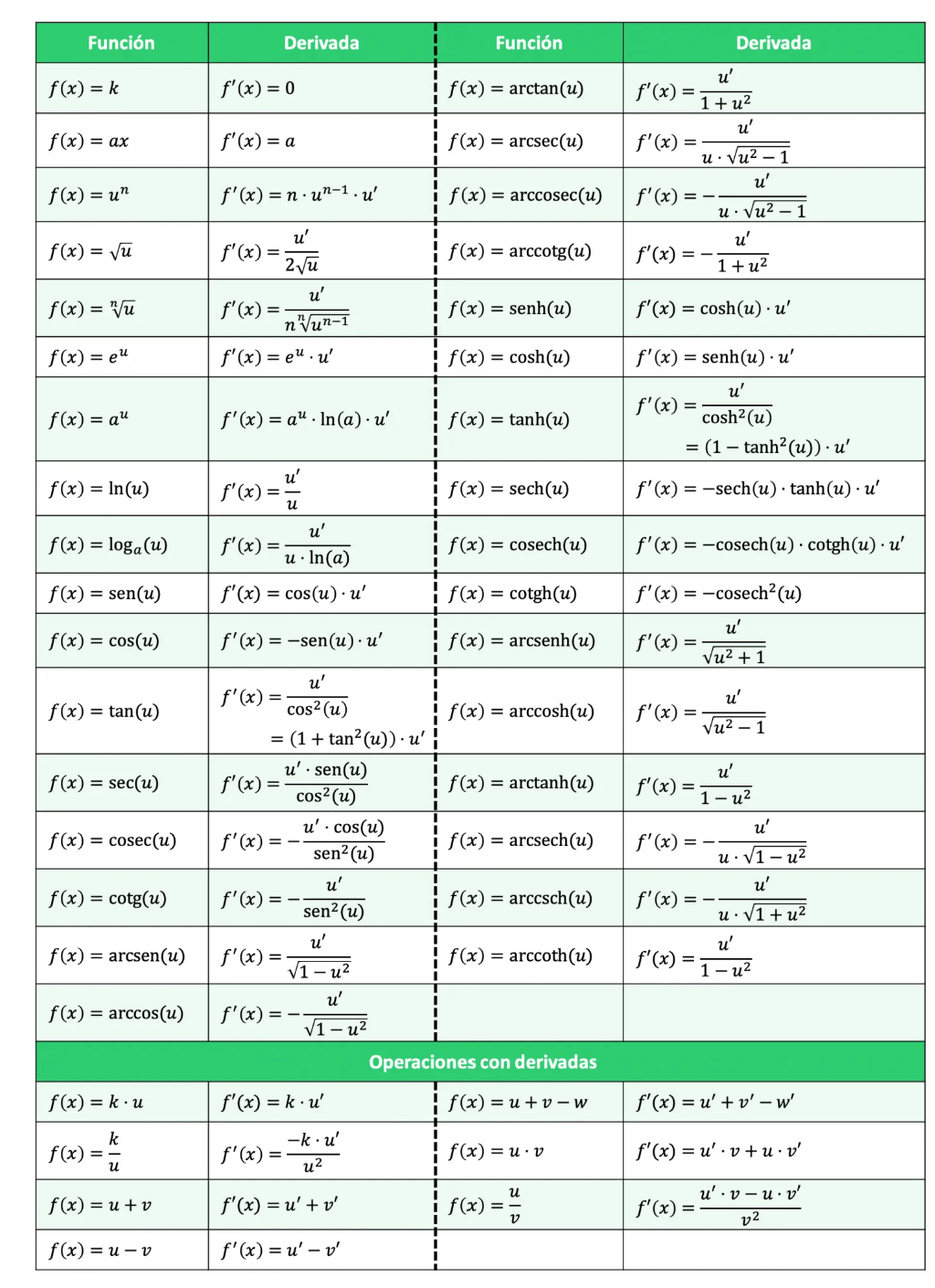
Recuerda en seguir practicando los conocimiento en funciones que ya has adquirido. La tabla de derivadas es solo un apoyo para reforzar los procesos matemáticos y de cálculo. Si necesitas ayuda, Luca estará en tu escuela para hacer tu proceso de aprendizaje aún más entretenido, completo y dinámico. Somos los aliados de las instituciones en la enseñanza y contamos con los mejores contenidos, ajustados a la malla curricular mexicana. Si quieres conocernos, visítanos aquí.





0 comentarios